Table of contents
- Stack Data Structure: Pancakes, Popsicles, and Properties
- Real-Life Applications of Stacks: From Pancakes to Programs
- Undo/Redo Operations: Ctrl+Z and Ctrl+Y
- Backtracking: Maze and Memory
- Expression Evaluation: Calculator and Code
- Implementation of Stack using Arrays and Linked Lists in Java
- Stack using Arrays
- Stack using Linked Lists
- Basic Operations of a Stack
- Examples of Common Stack Problems
- Summary
Have you ever played with a stack of pancakes? Yes, pancakes! Consider a stack of fluffy pancakes. Each with a unique topping: maple syrup, butter, blueberries, or chocolate chips. How would you eat them? Would you start from the top, the bottom, or the middle? Would you add more pancakes on top or remove some from the bottom? If you follow the Last-In-First-Out (LIFO) rule, you will eat the pancakes in the order they were stacked, starting from the top and working your way down, one by one. This is how a stack data structure works in computer science and programming.

A stack is a collection of elements that are arranged in a LIFO order, and you can push new elements on top of the stack or pop the top element of the stack. Stacks are not just tasty, but also very useful in algorithms and data structures.
In this blog post, we will explore the world of stacks in DSA, from their pancake-like properties to their real-world applications. Are you hungry for some stacks? Let's dig in!
Stack Data Structure: Pancakes, Popsicles, and Properties
A stack data structure is like a stack of pancakes, popsicles, or any other objects that can be stacked on top of each other. It has a few properties that make it very useful in computer science and programming:
LIFO: The Last-In-First-Out (LIFO) principle controls stacks. The last piece added to the stack is the first to be withdrawn. This is like eating a stack of pancakes from the top down or removing a popsicle from a stack by pulling it out from the top.
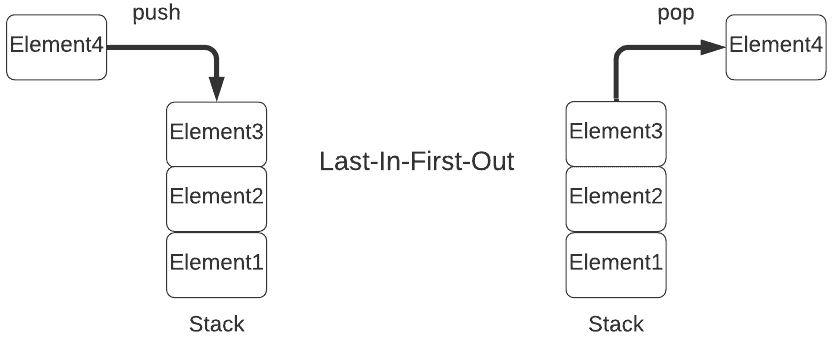
Push and Pop: Stacks confidently offer two essential operations that make them highly efficient: pushing an element to the top of the stack and popping the top element from it. It's like, how you add or remove a pancake from the top while enjoying a stack of them.
No Random Access: Stacks do not support random access to elements. You can only access the top element of the stack. This is similar to eating pancakes one at a time, beginning at the top and being unable to jump to the middle of the stack.
Stacks have many applications in algorithms and data structures, such as function call stacks, expression evaluation, backtracking, and memory management. Let's see how they work in practice and how we can implement them using arrays or linked lists.
Real-Life Applications of Stacks: From Pancakes to Programs
Stacks are a practical tool with numerous real-world applications, not only theoretical ideas in computer science and programming. Here are some examples that you may encounter in your daily life and how they relate to stacks:
Undo/Redo Operations: Ctrl+Z and Ctrl+Y

Have you ever made a mistake while typing a document or editing a photo and wished you could undo it with a magic wand? Most software applications' undo/redo operations function similarly to a stack. When you act, such as typing a letter, the software adds the action to a stack of actions. The software removes the last operation from the stack and undoes it when you click Ctrl+Z. If you press Ctrl+Z again, it undoes the previous move, and so on. If you press Ctrl+Y, the software redoes the last undone move by adding it back to the stack. This is like eating pancakes from the top down and, undoing the last one by removing it from the top and redoing it by adding it back to the top.
Backtracking: Maze and Memory

Have you ever played a maze game? Solved a puzzle and hit a dead end? It's frustrating, right? But fear not, my friend! Backtracking algorithms are here to save the day! They use STACKS to keep track of your moves and help you explore new paths. It's like a delicious pancake stack, but instead of eating them from the bottom up, you pop off the burnt ones and try the next delicious option! So, let's backtrack and conquer that maze or puzzle like the problem-solving champ you are!
Expression Evaluation: Calculator and Code
Have you ever used a calculator or written a program that evaluates mathematical expressions? The calculator or program parses and evaluates the statement using a stack in the order of operations. When you enter an expression, such as "2 + 3 * 4" the calculator or program converts it into a postfix notation, which can be evaluated using a stack.
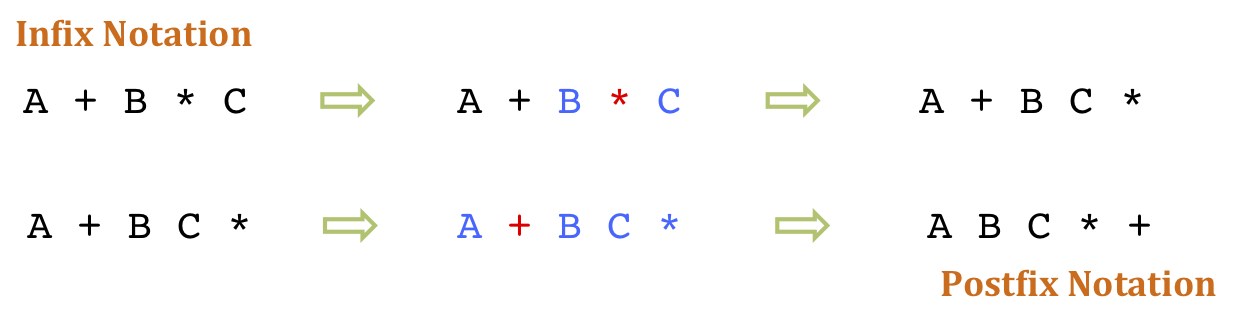
Each operand and operator is pushed onto the stack, and when an operator is encountered, the two top operands are popped from the stack, the operator is applied to them, and the result is pushed back onto the stack. This is like eating pancakes from the top down and evaluating the expression by adding and multiplying the numbers on the stack.
Stacks are used in computer science and programming, including function call stacks, memory allocation, and parsing. Understanding stacks are essential for mastering algorithms and data structures. Let's see how we can implement stacks using arrays and linked lists and optimize their performance and memory usage.
Implementation of Stack using Arrays and Linked Lists in Java
There are two main ways to implement a stack in Java: using an array or a linked list. Both methods have their pros and cons, depending on the application and the size of the stack.
Stack using Arrays
An array-based stack stores the elements in a fixed-size array and uses an index variable to keep track of the top element. Here's how you can implement a stack using an array in Java:
First, create a class for the stack.
public class StackArray { //here StackArray is a class.
private int[] elements;
private int top;
private int size;
// constructor
public StackArray(int capacity) {
elements = new int[capacity];
top = -1;
size = 0;
}
//push (means enter element into the stack)
public void push(int element) {
if (isFull()) {
throw new StackOverflowError("Stack is full");
}
top++;
elements[top] = element;
size++;
}
//pop (means delete element)
public int pop() {
if (isEmpty()) {
throw new EmptyStackException();
}
int element = elements[top];
top--;
size--;
return element;
}
//peek (means top element)
public int peek() {
if (isEmpty()) {
throw new EmptyStackException();
}
return elements[top];
}
// is stack empty?
public boolean isEmpty() {
return size == 0;
}
// or, is stack full?
public boolean isFull() {
return size == elements.length;
}
}
Let's go through each method step by step:
The constructor creates a new integer array with the specified capacity, sets the top index to -1 (indicating an empty stack), and sets the size to 0.
The push method adds a new element to the top of the stack, by incrementing the top index, storing the element at the corresponding array position, and incrementing the size. If the stack is already full, it throws a StackOverflowError.
The pop method removes the top element from the stack, by retrieving it from the array, decrementing the top index, decrementing the size, and returning the element. If the stack is already empty, it throws an EmptyStackException.
The peek method retrieves the top element from the stack, without removing it, by retrieving it from the array and returning it. If the stack is already empty, it throws an EmptyStackException.
The isEmpty method checks if the stack is empty, by comparing the size to 0 and returning a boolean value.
The isFull method checks if the stack is full, by comparing the size to the length of the array and returning a boolean value.
Stack using Linked Lists
A linked-list-based stack stores the elements in a dynamic linked list and uses a reference variable to keep track of the top element. Here's how you can implement a stack using a linked list in Java:
First, create a class for the stack node.
public class StackNode { int data; StackNode next; public StackNode(int data) { this.data = data; next = null; } }- The stack node contains the data for the element and a reference to the next node in the stack.
Create a class for the stack:
public class Stack { private StackNode top; // Push method public void push(int data) { StackNode newNode = new StackNode(data); newNode.next = top; top = newNode; } // Pop method public int pop() { if (isEmpty()) { throw new RuntimeException("Stack is empty"); } int data = top.data; top = top.next; return data; } // Peek method public int peek() { if (isEmpty()) { throw new RuntimeException("Stack is empty"); } return top.data; } // Check if stack is empty public boolean isEmpty() { return top == null; } }The stack contains a reference to the top node in the stack.
Implement the push method to add elements to the stack. First, create a new node with the given data. Set the next reference of the new node to the current top node. Set the top reference to the new node.
Implement the pop method to remove elements from the stack. First, check if the stack is empty with the isEmpty method. If it is, throw an exception. If not, remove the top element from the stack and set the top reference to the next node in the stack.
Implement the peek method to return the top element of the stack without removing it. First, check if the stack is empty with the isEmpty method. If it is, throw an exception. If not, return the top element.
Implement the isEmpty method to check if the stack is empty by checking if the top reference is null.
Basic Operations of a Stack
A stack is a linear data structure that follows the Last-In-First-Out (LIFO) principle. The basic operations of a stack include push, pop, peek, isEmpty, and isFull.
- Push operation:
The push operation adds an element to the top of the stack. It takes one parameter, which is the element to be added.
Here's a diagram that illustrates the push operation:
+---+ +---+
| 3 | | 3 |
+---+ push +---+
| 2 | ---> | 2 |
+---+ +---+
| 1 | | 1 |
+---+ +---+
empty after push
stack operation
And here's the corresponding code snippet in Java:
public void push(int element) {
if (isFull()) {
throw new StackOverflowError();
}
top++;
data[top] = element;
}
The push method checks if the stack is full before adding an element. If the stack is already full, it throws a StackOverflowError. Otherwise, it increments the top index and sets the value of the new top element to the specified element.
- Pop operation:
The pop operation removes the top element from the stack and returns its value. It does not take any parameters.
Here's a diagram that illustrates the pop operation:
+---+ +---+
| 3 | | |
+---+ pop +---+
| 2 | ---> | 2 |
+---+ +---+
| 1 | | 1 |
+---+ +---+
before after
pop pop
And here's the corresponding code snippet in Java:
public int pop() {
if (isEmpty()) {
throw new EmptyStackException();
}
int element = data[top];
top--;
return element;
}
The pop method checks if the stack is empty before removing an element. If the stack is already empty, it throws an EmptyStackException. Otherwise, it retrieves the value of the top element, decrements the top index, and returns the value.
- Peek operation:
The peek operation retrieves the value of the top element from the stack, without removing it. It does not take any parameters.
Here's a diagram that illustrates the peek operation:
+---+ +---+
| 3 | | 3 |
+---+ peek +---+
| 2 | ---> | 2 |
+---+ +---+
| 1 | | 1 |
+---+ +---+
before after
peek peek
And here's the corresponding code snippet in Java:
public int peek() {
if (isEmpty()) {
throw new EmptyStackException();
}
return data[top];
}
The peek method checks if the stack is empty before retrieving the value of the top element. If the stack is already empty, it throws an EmptyStackException. Otherwise, it returns the value of the top element.
- isEmpty operation:
The isEmpty operation checks if the stack is empty. It does not take any parameters.
Here's a diagram that illustrates the isEmpty operation:
+---+ empty
| | isEmpty stack
+---+
+---+ not empty
| 1 |
+---+ empty
| | isEmpty stack
+---+
And here's the corresponding code snippet in Java:
public boolean isEmpty() {
return top == -1;
}
The isEmpty method simply checks if the top index is -1, which indicates an empty stack. If the top index is not -1, it means there is at least one element in the stack, so it returns false.
- isFull operation:
The isFull operation checks if the stack is full. It does not take any parameters.
Here's a diagram that illustrates the isFull operation:
+---+ full
| 3 |
+---+
| 2 |
+---+
| 1 |
+---+
+---+ not full
| 3 |
+---+
| 2 |
+---+
| |
+---+
And here's the corresponding code snippet in Java:
public boolean isFull() {
return top == maxSize - 1;
}
The isFull method checks if the top index is equal to the maximum size of the stack minus 1, which indicates a full stack. If the top index is less than the maximum size minus 1, it means there is still space for at least one more element, so it returns false.
Examples of Common Stack Problems
Stacks are incredibly versatile data structures that can effectively tackle an extensive array of problems. Without a doubt, we will explore some of the most common problems solved using stacks in this section. Rest assured, I will be selecting these questions from Leetcode, the go-to platform for coding enthusiasts.
- Balancing Parentheses:
You can read and solve the question here.
The problem of balancing parentheses is a classic example of how stacks can be used to solve a real-world problem. It involves checking if a given expression has balanced parentheses or not. For example, the statement "(a+b)*(c-d)" has balanced parentheses while, "((a+b)" does not.
Solving this problem using a stack is a straightforward algorithm. The process involves iterating over every character in the expression and pushing any opening parenthesis onto the stack. For every closing parenthesis, we confidently check if the top of the stack matches the corresponding opening parenthesis. If it does, we pop the opening parenthesis from the stack. If it doesn't, the parentheses are not balanced.
Here's an example implementation in Java:
public boolean isBalanced(String expression) {
Stack<Character> stack = new Stack<>();
for (int i = 0; i < expression.length(); i++) {
char c = expression.charAt(i);
if (c == '(') {
stack.push(c);
} else if (c == ')') {
if (stack.isEmpty() || stack.pop() != '(') {
return false;
}
}
}
return stack.isEmpty();
}
- Problem: Given a string containing only '(' and ')', find the length of the longest valid (well-formed) parentheses substring. Leetcode
For example:
Input: "((())()" Output: 4 Explanation: The longest valid parentheses substring is "()()", which has a length of 4.
Algorithm:
Create a stack of integers to store the indices of opening parentheses.
Initialize a variable called maxLength to 0.
Initialize a variable called lastInvalid to -1.
Iterate through the string from left to right, and for each character:
a. If it's an opening parenthesis, push its index onto the stack.
b. If it's a closing parenthesis: i. If the stack is empty, update lastInvalid to the current index.
ii. Otherwise, pop the top index from the stack, and update maxLength to the maximum of itself and (current index - the top index of the stack or lastInvalid).
Return maxLength.
Here's the Java code implementation of the above algorithm:
public int longestValidParentheses(String s) {
Stack<Integer> stack = new Stack<>();
int maxLength = 0;
int lastInvalid = -1;
for (int i = 0; i < s.length(); i++) {
if (s.charAt(i) == '(') {
stack.push(i);
} else {
if (stack.isEmpty()) {
lastInvalid = i;
} else {
stack.pop();
if (stack.isEmpty()) {
maxLength = Math.max(maxLength, i - lastInvalid);
} else {
maxLength = Math.max(maxLength, i - stack.peek());
}
}
}
}
return maxLength;
}
Summary
In this blog, we discussed stack data structures in computer science. We explained what stacks are, their properties, and their real-life applications. We showed how to implement a stack using an array or a linked list in Java and explained the basic operations of a stack. We also discussed some common problems that can be solved using stacks, such as balancing parentheses and finding the length of the longest valid parentheses substring.
Key takeaways
Stacks are a fundamental data structure in computer science.
Stacks follow the Last-In-First-Out (LIFO) principle and support push, pop, peek, isEmpty, and isFull operations.
Stacks have many real-life applications, including undo/redo operations, backtracking, expression evaluation, etc.
Stacks can be implemented using arrays or linked lists in Java.
Stacks can solve various problems, including balancing parentheses, converting infix to postfix expressions, reversing a string or a linked list, and finding the length of the longest valid parentheses substring.
Conclusion
In conclusion, understanding stack data structures and their applications are essential for building efficient and elegant algorithms for various problems. We hope this blog has provided you with a solid foundation in stack data structures and inspired you to explore further.
To deepen your understanding and practice implementing stacks, I recommend solving problems on LeetCode and checking out Kunal Kushwaha's stack FAQ questions. These resources offer a wide range of practice problems and solutions for implementing stacks.
If you have any feedback or comments on this blog, please feel free to share them with me.
Resources
LeetCode: Stacks
Kunal Kushwaha: DSA Bootcamp Stacks
Connect with me
If you have any questions or want to connect with me, you can find me on Twitter, LinkedIn, or ShowwCase.
